插头DP学习笔记

Posted on |

什么是插头DP

插头DP通常用来解决一些奇奇怪怪的棋盘问题，比如给你一些限制条件，让你求棋盘上的一个环，或者一个特殊形状。本质上是一种状压DP，其实是状压DP的升级版。这里就拿学长推荐的毒瘤题神奇游乐园为例吧。

一些概念

插头

给你一个网格图，还有一个没完成的环路，你会发现有左端点和右端点，端点可以在网格的四个边上的任意一边，我们称左端点为左插头或者开插头，类似地，称右端点为右插头或者闭插头。

轮廓线

我们的DP是一格一格地进行的，完成了DP的网格和未进行DP的网格形成了一条分界线，这条分界线就是轮廓线。

如图所示：蓝色的是轮廓线，黄色的是正在进行DP的格子，绿色的是插头。

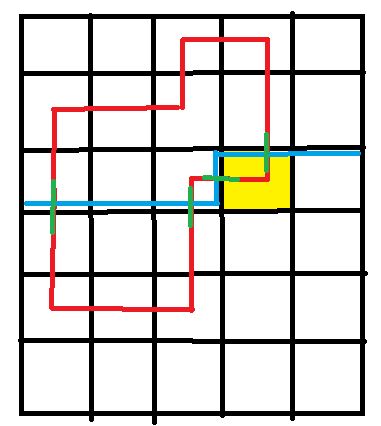
chatou1.JPG

如何进行DP

预处理

我们设 $f_{i,j,k}$ 表示当前处理格子为 $(i,j)$，状态为 $k$ 时最大的满意度之和（题目要求的）。

Q：等等，什么叫“状态为 $k$”？

A：这里，$k$ 是一个四进制数，每一位都代表着轮廓线上每一小段的状况，这一位为 $0$ 代表这一段没有插头（就像上图的第三行第二列），这一位为 $1$ 代表这一段有一个开插头（就像上图的第三行第一列），这一位为 $2$ 代表这一段有一个闭插头（就像上图的第二行第四列）。那么，上图的状态就是 101220 。

Q：既然没有 $3$，那为什么不用三进制？

A：辣你自己写三进制位运算啊！用四进制的好处就是，它可以和二进制联系起来，这样就不用预处理啦！具体来说就是，假如要取四进制下的第 $k$ 位，那就是二进制的第 $2k$ 位和第 $2k+1$ 位。

那现在就把代码写出来吧：

1
2
3
inline int get(int x,int k){//取出二进制状态 x 的第 k 位
    return (x>>(k<<1))&3;
}

Q：等等，这是什么鬼我看不懂啊！

A：那我解释一下：k<<1 意思就是 k*2 ，那么 x>>(k<<1) 意思就是状态 $x$ 的第 $2k$ 位，又由于前面说的，要取出 $2k$ 和 $2k+1$ 位，就和 3（在二进制下是 11​）进行按位与就行了。

状压DP的一个重要步骤就是预处理，所以我们先预处理出所有可行的状态。

Q：什么叫可行？

A：一个状态可行，那么它必须满足以下的条件：

  1. 不可能出现 3。（废话）
  2. 从左往右扫，遇到一个闭插头，就必须与他左边最近的未配对的的开插头配对。（仔细想想为什么）
  3. 所有插头都配对了。（废话）

我们用 s[] 数组记录插头的位置，Map[i][j] 表示状态 $i$ 下 $j$ 配对的插头，sta[] 记录合法的状态。

那么写出代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
inline void prework(){
    maxk=1<<((m+1)<<1);//我知道你可能对此不理解，请看注解1
    for(int k=0;k<maxk;++k){
        bool flag=true;//flag=true 表示这种状态是合法的
        sp=0;//表示这种状态有几个开插头
        for(int j=0,cur;j<=m;++j){//从左往右扫
            cur=get(k,j);//轮廓线上这一段是什么
            if(cur==3){flag=false;break;}//合法的状态不会出现3
            if(cur==2){//这是个闭插头
                if(sp<=0){flag=false;break;}//没有可以配对的插头，状态不合法
                Map[k][j]=s[sp];//遇到一个闭插头，就必须与他左边最近的未配对的的开插头配对
                Map[k][s[sp]]=j;
                sp--;//可以配对的开插头减一
			}
            else if(cur==1)s[++sp]=j;//这是一个新的开插头
        }
        if(flag&&sp==0)sta[++cnt]=k;//合法的话记录这个状态
	}
}

注解1：maxk=1<<((m+1)<<1) 用数学语言表达就是 $maxk=2^{2(m+1)}=4^{m+1}$ ，表示有多少种状态；是 m+1 而不是 m 是因为轮廓线的长度是 m+1 而不是 m （因为有一个小拐弯）。

递推过程

接下来是重头戏，也就是递推过程。状态转移需要分很多情况。

我们令 cur 为当前格上插头的状态，last 为当前格左插头的状态。

情况一：cur==0&&last==0

将当前格的下插头设为新的开插头，当前格右插头设为新的闭插头。

情况二：cur==0||last==0

两种方法：

  1. 把插头拉到格子右边，右插头的值就是原插头的值。
  2. 把插头拉到格子下边，下面的插头的值就是原插头的值。

情况三：cur==2&&last==1

一条环路结束了，更新答案。

情况四：cur==1&&last==2

删去插头代表的回路。

情况五：cur==last

两个插头同开同闭。那么首先清空匹配，然后重新分配。

具体来说，如果是两个闭插头在一起，把 last 对应的开插头改成闭插头；如果是两个开插头在一起，把 cur 对应的闭插头改成开插头。

不清楚的话可以在纸上模拟一下。

递推过程的代码

那么下面是递推过程的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
inline void Update(int &x,int k){
    if(x<k)x=k;
}
inline void solve(){
    for(int i=1;i<=n;++i){
        for(int K=1,k;K<=cnt;++K){//对于每一种可行的状态
            k=sta[K];
            if(f[i-1][m][k]!=-inf&&get(k,m)==0)//导入上一行的扫描线：如果上一行的这个状态被更新过而且上一行这一个状态的轮廓线的这个位置并不是什么都没有
            f[i][0][k<<2]=f[i-1][m][k];
        }
        for(int j=1;j<=m;++j){
            Update(f[i][j][(1<<((j-1)<<1))|(2<<(j<<1))],a[i][j]);//初始化
            for(int K=1,k,ck,cur,last;K<=cnt;++K){
                k=sta[K];
                if(f[i][j-1][k]==-inf)continue;//非法情况
                ck=k&(~(3<<((j-1)<<1)))&(~(3<<(j<<1))); //获得下一位置状态的模板，空出 j-1 和 j 位以填写
                cur=get(k,j);last=get(k,j-1);//插头状态
                if(cur==0&&last==0){//情况一
                    Update(f[i][j][k],f[i][j-1][k]);//什么也不放
                    Update(f[i][j][ck|(1<<((j-1)<<1))|(2<<(j<<1))],f[i][j-1][k]+a[i][j]);//在 j-1 和 j 插入 1 和 2，代表将当前格的下插头设为新的开插头，当前格右插头设为新的闭插头
                }
                else if(cur==0||last==0){//情况二
                    int t=max(cur,last);//选出不为空的
                    //接下来两种方法
                    Update(f[i][j][ck|(t<<((j-1)<<1))],f[i][j-1][k]+a[i][j]);
                    Update(f[i][j][ck|(t<<(j<<1))],f[i][j-1][k]+a[i][j]);
                }
                else if(cur==2&&last==1){//情况三
                    if(!ck)//如果确实是个回路
                     Update(res,f[i][j-1][k]+a[i][j]);//更新答案
                }
                else if(cur==1&&last==2){
                    Update(f[i][j][ck],f[i][j-1][k]+a[i][j]);//删去这两个插头代表的回路
                }
                else if(cur==last){
                    int t=ck&(~(3<<(Map[k][j-1]<<1)))&(~(3<<(Map[k][j]<<1)));//清空匹配
                    t=t|(1<<(Map[k][j]<<1))|(2<<(Map[k][j-1]<<1));//重新匹配
                    Update(f[i][j][t],f[i][j-1][k]+a[i][j]);
                }
            }
        }
    }
    cout<<res<<endl;
}

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
#include<bits/stdc++.h>
using namespace std;
const int maxn=110;
const int maxm=20;
const int maxs=(1<<14);
const int inf=1e9;
int f[maxn][maxm][maxs],a[maxn][maxm];
int Map[maxs][maxm],sta[maxs],cnt=0,s[maxs],sp;
int n,m,maxk,res=-inf;
inline int get(int x,int k){//取出二进制状态 x 的第 k 位
    return (x>>(k<<1))&3;
}
inline void prework(){
    maxk=1<<((m+1)<<1);//我知道你可能对此不理解，请看注解1
    for(int k=0;k<maxk;++k){
        bool flag=true;//flag=true 表示这种状态是合法的
        sp=0;//表示这种状态有几个开插头
        for(int j=0,cur;j<=m;++j){//从左往右扫
            cur=get(k,j);//轮廓线上这一段是什么
            if(cur==3){flag=false;break;}//合法的状态不会出现3
            if(cur==2){//这是个闭插头
                if(sp<=0){flag=false;break;}//没有可以配对的插头，状态不合法
                Map[k][j]=s[sp];//遇到一个闭插头，就必须与他左边最近的未配对的的开插头配对
                Map[k][s[sp]]=j;
                sp--;//可以配对的开插头减一
			}
            else if(cur==1)s[++sp]=j;//这是一个新的开插头
        }
        if(flag&&sp==0)sta[++cnt]=k;//合法的话记录这个状态
	}
}
inline void Update(int &x,int k){
    if(x<k)x=k;
}
inline void solve(){
    for(int i=1;i<=n;++i){
        for(int K=1,k;K<=cnt;++K){//对于每一种可行的状态
            k=sta[K];
            if(f[i-1][m][k]!=-inf&&get(k,m)==0)//导入上一行的扫描线：如果上一行的这个状态被更新过而且上一行这一个状态的轮廓线的这个位置并不是什么都没有
            f[i][0][k<<2]=f[i-1][m][k];
        }
        for(int j=1;j<=m;++j){
            Update(f[i][j][(1<<((j-1)<<1))|(2<<(j<<1))],a[i][j]);//初始化
            for(int K=1,k,ck,cur,last;K<=cnt;++K){
                k=sta[K];
                if(f[i][j-1][k]==-inf)continue;//非法情况
                ck=k&(~(3<<((j-1)<<1)))&(~(3<<(j<<1))); //获得下一位置状态的模板，空出 j-1 和 j 位以填写
                cur=get(k,j);last=get(k,j-1);//插头状态
                if(cur==0&&last==0){//情况一
                    Update(f[i][j][k],f[i][j-1][k]);//什么也不放
                    Update(f[i][j][ck|(1<<((j-1)<<1))|(2<<(j<<1))],f[i][j-1][k]+a[i][j]);//在 j-1 和 j 插入 1 和 2，代表将当前格的下插头设为新的开插头，当前格右插头设为新的闭插头
                }
                else if(cur==0||last==0){//情况二
                    int t=max(cur,last);//选出不为空的
                    //接下来两种方法
                    Update(f[i][j][ck|(t<<((j-1)<<1))],f[i][j-1][k]+a[i][j]);
                    Update(f[i][j][ck|(t<<(j<<1))],f[i][j-1][k]+a[i][j]);
                }
                else if(cur==2&&last==1){//情况三
                    if(!ck)//如果确实是个回路
                     Update(res,f[i][j-1][k]+a[i][j]);//更新答案
                }
                else if(cur==1&&last==2){
                    Update(f[i][j][ck],f[i][j-1][k]+a[i][j]);//删去这两个插头代表的回路
                }
                else if(cur==last){
                    int t=ck&(~(3<<(Map[k][j-1]<<1)))&(~(3<<(Map[k][j]<<1)));//清空匹配
                    t=t|(1<<(Map[k][j]<<1))|(2<<(Map[k][j-1]<<1));//重新匹配
                    Update(f[i][j][t],f[i][j-1][k]+a[i][j]);
                }
            }
        }
    }
    cout<<res<<endl;
}
int main(){
    ios::sync_with_stdio(0);
    cin>>n>>m;
    for(int i=1;i<=n;++i)
     for(int j=1;j<=m;++j)
      cin>>a[i][j];
    prework();
    for(int i=0;i<=n;++i)
     for(int j=0;j<=m;++j)
      for(int k=0;k<maxk;++k)
       f[i][j][k]=-inf;
    solve();
    return 0;
}
0%